COMPUTER NETWORKS

CONE home

general info

course contents

class schedule

instructor

students

news

exams

theses

archive

faq

links

contacts

CONE theory

CONE lab

CONE Lab - Computer Networks and Internet - Numerical exercises

Solution to Problem 2 (by J.F. Kurose and K.W. Ross)

a) A circuit-switched network would be well suited to the application described, because the application involves long sessions with predictable smooth bandwidth requirements. Since the transmission rate is known and not bursty, bandwidth can be reserved for each application session circuit with no significant waste. In addition, we need not worry greatly about the overhead costs of setting up and tearing down a circuit connection, which are amortized over the lengthy duration of a typical application session.

b) Given such generous link capacities, the network needs no congestion control mechanism. In the worst (most potentially congested) case, all the applications simultaneously transmit over one or more particular network links. However, since each
link offers sufficient bandwidth to handle the sum of all of the applications' data rates, no congestion (very little queueing) will occur.

Solution to Problem 5 (by J.F. Kurose and K.W. Ross)

a) The time to transmit one packet onto a link is (L + h) / R. The time to deliver the first of the M packets to the destination is Q * (L + h) / R . Every (L + h) / R seconds a new packet from the M - 1 remaining packets arrives at the destination. Thus the total latency is t_s + (Q + M - 1) * (L + h) / R

b) (Q + M - 1) * (L + 2h) / R

c) The time required to transmit the message over one link is (LM + 2h) / R . The time required to transmit the message over Q links is Q * (LM + 2h) / R

d) Because there is no store-and-forward delays at the links, the total delay is t_s + (ML + h) / R

Solution to Problem 7 (by J.F. Kurose and K.W. Ross)

a) d_prop = m / s seconds.

b) d_trans = L / R seconds.

c) ) d_end-to-end = (m / s + L / R) seconds.

d) The bit is just leaving Host A.

e) The first bit is in the link and has not reached Host B.

f) The first bit has reached Host B.

g) Want
m = ( L / R) * S = (100 / 28 * 10³) * (2.5 * 10⁸) = 893 km

Solution to Problem A
a)

b)

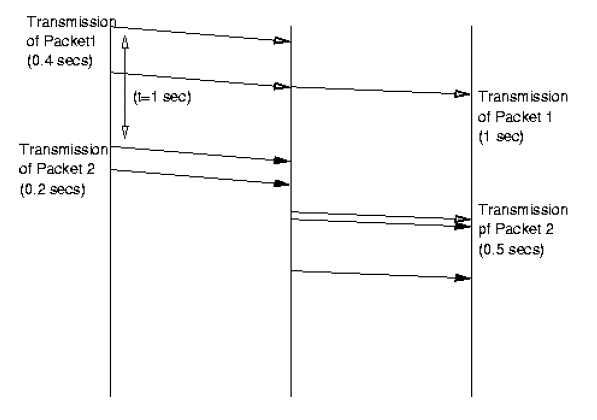
Solution to Problem B
(a) The packet size is the size of data + the size of header = (400 + 56) bits = 456 bits.
Time to transmit 456 bits = 456/56k = 8.14ms.
The transmission of N packets over 10 links takes, N*8.14ms + 9*8.14ms.
Adding the setup-up time, the total delay is 400ms + N*8.14ms + 9*8.14ms = 473ms + N*8.14ms.

(b) The packet size is the size of data + the size of header = (400 + 96) bits = 496 bits.
Time to transmit 496 bits = 496/56k = 8.86ms.
The transmission of N packets over 10 links takes, N*8.86ms + 9*8.86ms.
There is no setup time. As a result, the total delay is N*8.86ms + 79.74ms.

(c) The two are almost equal when N = 548.
Therefore, for messages that are shorter than 548 packet, use datagram transport.
Otherwise, use virtual-circuit service.

Solution to Problem C
(a) The minimum RTT is two times of the propagation delay on the link = 2*385,000,000m / (3*10^8 m/s) = 2.57s.

(b) The delay-bandwidth product = (2.57 s)*(100 Mbits/s) = 257Mbits = 32M bytes.

(c) Same as the delay bandwidth product.

(d) It would then take (1/2) RTT for the earth to make the download request and another (1/2) RTT for the propagation delay for sending the data from the moon to the earth. The total time is the sum of the transmission time and the two (1/2) RTT.
Minimum amount of time = 25MB/100Mbps + (1/2) RTT + (1/2) RTT
= 200Mb/100Mbps + 2.57 s
= 2 s + 2.57s
= 4.57s